Category: Macro

Macro

Current account equilibria in AEs

Post author By Paul Della Guardia
Post date 2024-01-24
Tags AEs

Have you ever wondered what a country’s current account balance should be? If you’re a macroeconomist or investor, then chances are that you have. While plenty has been written on how to measure “equilibrium” current account balances, to my knowledge there is precious little publicly-available information as to what these actually are. So I’ve drawn from the existing literature on the subject in an attempt to construct a model of where a country’s current account should stand over the medium-to-long term.

If you’re asking yourself why you should care about “normal” current account balances, first of all a quick refresher. The current account is the sum of a country’s goods and services trade balances (i.e. exports minus imports), its net primary income (e.g. wages and investment income from abroad), and net secondary income (i.e. grants from foreign donors and workers’ remittances from abroad). Adding consumption and investment to the current account is equal to gross national income, and some simple arithmetic shows that the CAB is also equivalent to savings minus investment:

CAB = PIB + SIB + X - M

GNI = PIB + SIB + X - M + C + I = CAB + C + I

CAB = GNI - C - I = S - I

From a savings minus investment perspective, the CAB is the sum of the public sector’s (i.e. government) S - I balance, which is closely related to the government’s budget, and the private sector’s S - I balance. Surplus current account flows lead to the accumulation of foreign currency reserves and/or net foreign assets acquisition, while a deficit must be financed by capital from abroad and/or the depletion of the central bank’s foreign currency reserves.

Exchange rates

Exchange rates obviously play a pivotal role in influencing a CAB, which is why “currency wars” periodically erupt, with nations accusing each other – sometimes with good reason – of artificially devaluing their currencies in order to boost their CABs. Currencies are also one of the main reasons to take an interest in CABs, because the latter help measure whether a currency is over- or undervalued.

Focusing on a country’s real effective exchange rate, i.e. its trade-weighted exchange rate incorporating relative price levels of its trading partners, there are multiple approaches to assessing REER fair value, one of which involves measuring cyclically-adjusted (i.e. “underlying”) current account deviations from the equilibrium current account:

REER deviation from FV ≈ CAB_underlying - CAB_equilibrium

Undervalued currency: CAB_underlying > CAB_equilibrium

Overvalued currency: CAB_underlying < CAB_equilibrium

CAB modeling results

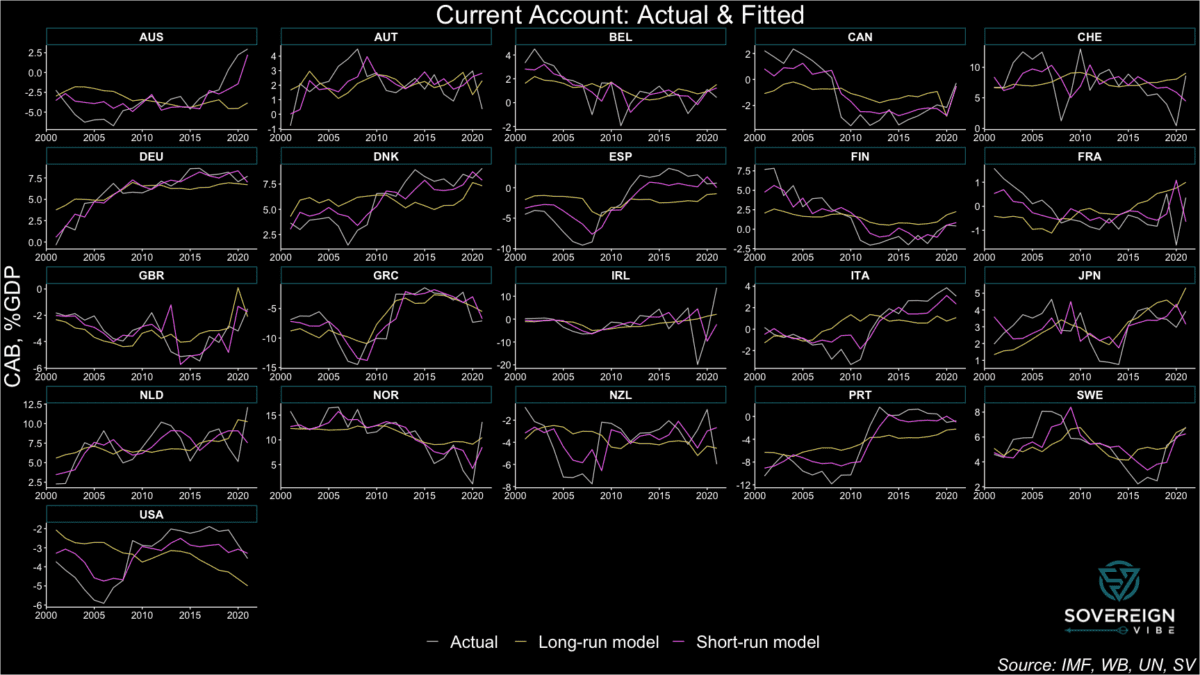
The first step in this analysis is to measure equilibria CABs that reflect a country’s non-cyclical characteristics over the medium-to-long run, hewing closely to past work on the subject, including by analyzing the same group of 21 advanced economies. I’ve developed two models in order to track these CABs: short-run estimates of observed CAB readings and a long-run framework to approximate equilibria CABs.

The results are presented in the chart below, featuring CAB observations, the long-run model, and short-run model. The latter tracks the actual CAB results relatively closely, in large part because the cyclical/short-term variables exhibit high degrees of statistical significance in the model. Moreover, the observed CAB values are obviously driven by cyclical factors in addition to long-term trends.

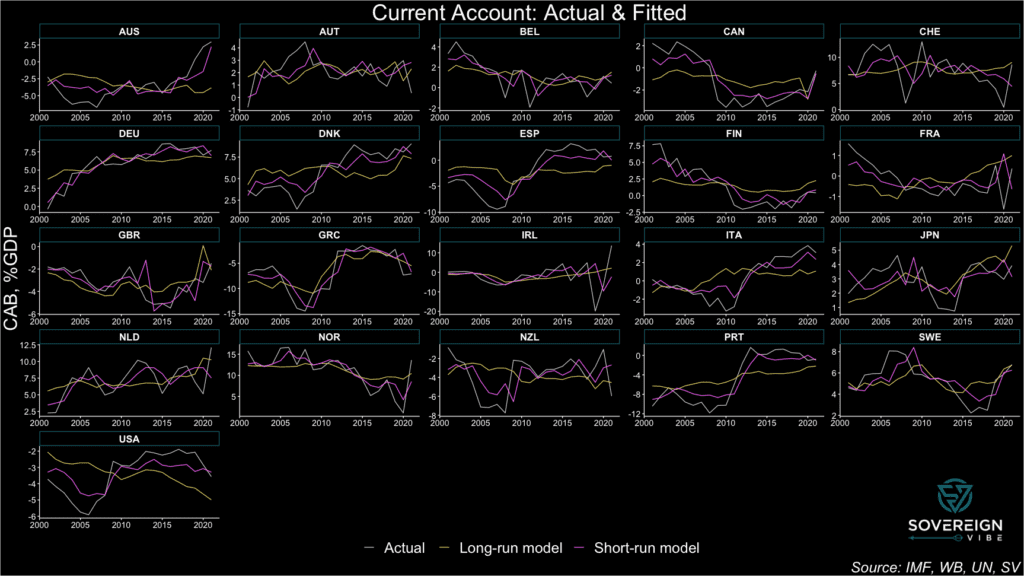
In contrast, the long-run model has much lower explanatory power compared to the short-run model with respect to minimizing residual deviations away from the observed CABs. But this is precisely the point. Medium- to long-run CAB equilibria should be relatively stable compared to the cyclical volatility exhibited by the actual CABs and their short-run fitted values.

Still, the long-run model estimates of CAB equilibria are subject to a high degree of uncertainty, given the the presence of statistical significance in only one of the three independent variables and low adjusted R² (see regressions below).

Model & variable selection

The analysis uses panel data for 21 advanced economies from 2001 – 2021 and included various statistical tests for selecting appropriate models and controlling for heteroskedasticity, serial correlation, cross-sectional dependence, and stationarity. For both the short- and long-run approaches, fixed effects models were chosen over OLS or random effects. Only individual (i.e. country) fixed effects were included; time-fixed effects were unnecessary.

The current account balance as a percentage of nominal GDP served as the dependent variable for both the short- and long-run frameworks.

Short-run model variables

One-year lag of the dependent variable, i.e. the current account / GDP ratio. The high degree of inertia in CAB time series processes resulted in a large positive coefficient at a high degree of significance.
Deviation from the in-sample average of the general government cyclically-adjusted budget balance adjusted for nonstructural elements beyond the economic cycle, as a share of potential GDP. Countries with higher-than average government budget balances should be able to attract larger portions of global current account surpluses. This is confirmed by the positive coefficient at 1% significance.
Deviation from the in-sample average of GNI per capita on a PPP basis, adjusted for the country’s output gap to equate the observation to what it would be if the economy were running at potential. As expected, the coefficient is positive – reflecting the CAB-GNI conceptual overlap, greater availability of income and thus savings opportunities to wealthier countries, and the need for capital deepening in less developed countries. It is significant when standard errors are adjusted for heteroskedasticity and autocorrelation in this fixed effects model.
Domestic output gap: actual output minus potential output in current USD (logarithmic difference). Economies in the boom phase of an economic cycle can experience strong import growth, appreciated exchange rates, and stronger remittance and primary income outflows, putting the current account under pressure. As expected, the coefficient is negative, large, and significant.
One-year change in the terms of trade, i.e. the ratio of the price of exports to the price of imports. The coefficient is positive and significant, as expected.
One-year change in the REER. The coefficient is negative and significant, as expected, because high REERs can lead to imports becoming relatively cheap, thus increasing import volumes, and lead to exports becoming relatively expensive, thus decreasing export volumes.

**Regression Results – 21 Advanced Economies**

	Dependent variable:

	Current Account Balance, %GDP
	panel	coefficient
	linear	test
	(1)	(2)
	fixed.shortrun	fixed.hac.shortrun

cab.t_1	0.582^***	0.582^***
	(0.040)	(0.125)
sur_dev	0.221^***	0.221^**
	(0.052)	(0.089)
ypcap_dev	0.026	0.026^**
	(0.018)	(0.011)
ogap_usd.logdiff	-6.593^*	-6.593^*
	(3.994)	(3.620)
tot_1d	0.091^***	0.091^**
	(0.021)	(0.044)
reer_1d	-0.050^*	-0.050^**
	(0.028)	(0.024)

Observations	441
R²	0.456
Adjusted R²	0.422
F Statistic	57.907^*** (df = 6; 414)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Long-run model variables

Deviation from the in-sample average of the general government cyclically-adjusted budget balance adjusted for nonstructural elements beyond the economic cycle, as a share of potential GDP. Countries with higher-than average government budget balances should be able to attract larger portions of global current account surpluses. This is confirmed by the positive coefficient at 1% significance.
The deviation from the in-sample average of total dependency ratio of non-workers on the 20-64 year-old working-age population, i.e. people 19 and under & 65 and over. Faruqee and Isard contend that the dependency ratio should be negatively associated with current account equilibria, partly due to the income effect, and find it to be so in their 1970s – 1990s data. Here the sign is positive, somewhat unexpectedly, and is statistically insignificant.
The deviation from the in-sample average of the child-age dependency ratio on the 20-64 year-old working-age population, i.e. people 19 and under. I tested this variable on the intuition that the child dependency ratio could well be negative, not only due to the income effect as noted by Faruqee and Isard, but also due to the large amounts of consumption (which pushes down savings, increases imports etc) associated with children’s parents at the height of their income generation, family activities, and the associated demographic profile that such countries might have. Although this relationship showed up as negative in OLS, in this fixed effects model it is insignificant and unexpectedly positive.
The deviation from the in-sample average of the old-age dependency ratio on the 20-64 year-old working-age population, i.e. people 65 and over. My intuition with this variable is that it would be positive because of the high level of savings that elderly people have, despite doubts as to the degree to which the elderly can generate positive savings flows for themselves. The sign was positive, as expected, but small and insignificant.
Deviation from the in-sample average of GNI per capita on a PPP basis, adjusted for the country’s output gap to equate the observation to what it would be if the economy were running at potential. As expected, the coefficient is positive – reflecting the CAB-GNI conceptual overlap, greater availability of income and thus savings opportunities to wealthier countries, and the need for capital deepening in less developed countries. Yet this result is weak and insignificant in the long-run model.

**Regression Results – 21 Advanced Economies**

	Dependent variable:

	Current Account Balance, %GDP		cab_ngdp
	panel	coefficient	panel	coefficient
	linear	test	linear	test
	(1)	(2)	(3)	(4)
	fixed.longrun.a	fixed.hac.longrun.a	fixed.longrun.b	fixed.hac.longrun.b

sur_dev	0.481^***	0.481^***	0.478^***	0.478^***
	(0.062)	(0.125)	(0.062)	(0.129)
dem_tot_dev	0.086	0.086
	(0.067)	(0.134)
dem_chd_dev			0.173	0.173
			(0.143)	(0.361)
dem_old_dev			0.048	0.048
			(0.087)	(0.162)
ypcap_dev	0.014	0.014	0.012	0.012
	(0.023)	(0.035)	(0.023)	(0.038)

Observations	441		441
R²	0.148		0.149
Adjusted R²	0.101		0.100
F Statistic	24.141^*** (df = 3; 417)		18.201^*** (df = 4; 416)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

Post author By Paul Della Guardia
Post date 2024-01-24
Categories In Macro
Tags AEs
1 Comment on Current account equilibria in AEs

Macro

Mapping the world’s output gaps

Post author By Paul Della Guardia
Post date 2023-12-14
Tags AEs, EMDEs, LICs

Building on recent work on how to measure deviations of actual GDP from potential GDP, known as an output gap, I’m pleased to reveal a world map of results for 2023. Remember that an output gap is positive when actual GDP is above potential – or trend – and negative when it is below. In the map below, countries in blue have positive output gaps in 2023, while those in orange and red are negative.

While most countries are exhibiting above-trend GDP growth, there are some noteworthy pockets of below-trend output. Chief among these is a large negative output gap in Ukraine, clearly related to the ongoing war with Russia, and which also appears to have infected several of its neighbors in north-eastern and north-central Europe.

Other countries with active conflicts or security-related concerns also seem to be well below potential: Sudan, Myanmar, Haiti, and Iraq.

There are also some clusters of negative gaps in various regions: Latin America (Peru, Bolivia, Paraguay, and Chile), South/Southeast Asia (Pakistan, Nepal, Bhutan, Myanmar, Thailand, Laos), and West-Central Africa (Ghana, Burkina Faso, Gabon).

As for the positive output gaps around the world, these are mostly in the range of 0-2.5% of potential GDP. Much of southern Europe is above this level: Portugal, Spain, Italy, Croatia, Montenegro, Albania, Greece. Farther east, Georgia, Armenia, Iran, and Tajikistan have also recorded above-trend output beyond 2.5%. Brazil and some parts of Africa (Libya, Republic of Congo, Democratic Republic of Congo, Botswana, Benin, and Liberia).

The countries with the largest positive output gaps are in darkest blue: Guyana, Yemen, and Libya. The latter two have of course experienced significant conflicts over the past decade, suggesting that actual GDP is now well above trend as a result of those previous shocks. High positive output gaps can also be a symptom of economic overheating.

Note that data for 2023 is absent for some countries in the map because the IMF did not provide actual GDP estimates for this year in its October 2023 World Economic Outlook. These include Sri Lanka, Afghanistan, Syria, Venezuela, and Cuba. Given high economic uncertainty and/or the absence of reliable data from these countries, fair enough.

Trend GDP: a visual primer

So far in my writing about output gaps I haven’t made any visual presentations of what real and potential GDP look like. As explained previously, measuring potential GDP is complicated and data-intensive, so economists often use a shortcut: deriving a moving average of actual GDP readings as a proxy for potential GDP. The approach I have taken is known as Hodrick-Prescott filtering.

As a result of the previously-noted pitfalls of using moving averages to measure potential GDP, I refer to the term of “trend” rather than “potential” GDP. As for “actual” GDP, this is data in national currency units using constant prices, meaning that it is real – and not nominal – GDP.

The charts below provide examples actual and trend GDP. I’ve selected these countries because they are ongoing sovereign debt restructuring cases of interest, even if I only present them here for demonstrating how actual / real and trend / potential GDP relate to each other and output gaps:

Output Gap = (Real GDP - Potential GDP) / Potential GDP * 100

Sri Lanka is perhaps the most interesting case, even if the data is only through 2022: a sizable positive output gap – indicating potential overheating in the economy – preceded a sharp drop in GDP, leading to a negative output gap. Also currently in negative territory, Ghana’s GDP exhibits some of the same behavior, albeit with less volatility.

Zambia sustained a positive output gap throughout most of the 2010s, until an economic contraction in 2020 led it into negative territory, though the gap turned positive again in 2023. Once one of the world’s fastest growing economies, Ethiopia’s economic growth has also been remarkably stable, despite the recent Tigray conflict. This makes for a more “boring” chart but is a credit to the country’s economy, with the output gap in marginally positive territory.

Post author By Paul Della Guardia
Post date 2023-12-14
Categories In Macro
Tags AEs, EMDEs, LICs
2 Comments on Mapping the world’s output gaps

Macro

On a quest for output gaps

Post author By Paul Della Guardia
Post date 2023-11-24

One of the holy grails in the economics profession is to accurately measure an economy’s output gap, which is the difference between its actual GDP and potential GDP. Having an accurate representation of an output gap is useful for all sorts of economic modeling purposes, given statistical relationships with inflation, exchange rates, and a host of other variables of interest to economists, investors, and policymakers. Simply put, a positive (negative) output gap means that actual GDP is above (below) potential GDP.

Yet the IMF in its flagship World Economic Outlook database provides output gaps for fewer than 30 advanced economies, to say nothing of emerging and developing economies. The Fund does of course in many cases provide such estimates elsewhere, such as in country and program monitoring reports, but, unfortunately, leaves these out of the WEO.

Measuring output gaps is notoriously riddled with uncertainty because, unlike actual GDP, potential GDP isn’t directly observed through spending or income. Rather, it needs to be estimated in some other way, which I have done for the broadest possible group of advanced and emerging-developing economies.

The optimal approach for calculating potential GDP likely focuses on supply side inputs including total factor productivity, labor, and capital à la Y = AL^αK^1−α, an example of which is the Production Function Methodology. Yet such methodologies can be data-intensive, especially when looking at emerging and developing economies, for which data is often scarcer.

An alternative is to use a moving averages approach – one of which is known as Hodrick-Prescott filtering – that separates actual GDP readings into trend and cyclical components, representing potential output and the output gap, respectively. One of the downsides of this approach is that it may misestimate potential output by ignoring the individual supply-side constituents used in bottom-up methodologies. An advantage of HP filtering is that potential GDP and output gaps can be quickly estimated for a broad group of countries from real GDP data.

The problem is of course whether the HP-estimated output gaps that I have prepared are actually any good. To assess this, I compare the HP results with the countries – all of which are advanced economies – for which the IMF provides output gap estimates in its World Economic Outlook database. Using the October 2023 WEO, I derive the HP output gaps for many countries with annual real GDP readings and λ = 100. I rely on data in national currency, which has the benefit of minimizing exchange rate effects that are present in USD data. I then plot the HP-derived output gaps against the IMF’s own output gap estimates, hoping to see something resembling a positive, one-to-one relationship, which the data bear out fairly well:

Behind the scenes I’ve looked at slopes by individual countries (remember m = Δy/Δx), and these all seem to be m < 1, indicating that there is more variance in the HP-derived output gaps. In any case, these data seem to track pretty closely, meaning that the HP gaps probably have some analytical value.

Next, I put the WEO and HP output gaps to the test separately against inflation readings, expecting the relationship to be positive. The theoretical underpinning is that when an economy is running hot – i.e. its output gap is positive – prices tend to rise more. Known as the Phillips Curve, this relationship is also often shown as the negative link between inflation and unemployment.

The two faceted charts below show Phillips Curves for the selected countries where IMF output gap estimates are available in the WEO. The first one uses the IMF’s output gap estimates in the x-axis, while the second one uses the HP-derived ones. Consistently positive relationships likely point to better output gap measurement.

In the first chart, the WEO’s output gap estimates point to a positive relationship with inflation in most countries, as per the fitted linear regression lines. There are, however, some exceptions. Austria, Belgium, Spain, Japan, Korea, and possibly Denmark all exhibit negative relationships. Others such as Slovakia, Estonia, and Norway appear quite flat. This calls into question the IMF’s output gap estimates in these countries, according to the Fund’s own data.

On the other hand, the second chart exhibits more consistently-positive relationships with inflation in this sample of countries, suggesting that the HP-derived output gaps may actually be more accurate than those provided by the IMF. Slovakia appears to be the only country with a negatively-sloped line, although admittedly Estonia, Italy, and Portugal are nearly flat.